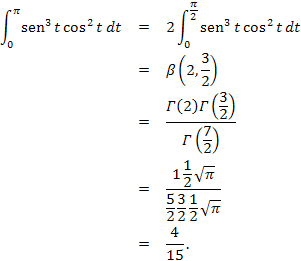La función Beta y las integrales de productos de senos y cosenos
Entre las propiedades de la función Beta, queremos llamar la atención sobre una de ellas, que nos permite expresar dicha función como el doble de la integral en ![]() del producto de potencias de seno y coseno. Nos referimos a la propiedad (3):
del producto de potencias de seno y coseno. Nos referimos a la propiedad (3):
![]()
Las funciones seno y coseno, sus potencias y el producto de potencias de funciones seno y coseno, presentan una singularidad en los intervalos de la forma ![]() , donde
, donde ![]() y
y ![]() son números enteros cualesquiera, con
son números enteros cualesquiera, con ![]() . Vamos a precisar en ello, para lo cual, consideramos primero las funciones seno y coseno por separado.
. Vamos a precisar en ello, para lo cual, consideramos primero las funciones seno y coseno por separado.

Figura 1.5.1 Representaciones gráficas de las funciones seno y coseno.
En la Figura 1.5.1 podemos ver las gráficas de las curvas ![]() e
e ![]() en el intervalo
en el intervalo ![]() . Como ya sabemos, ambas funciones son periódicas de período
. Como ya sabemos, ambas funciones son periódicas de período ![]() . Pero hay algo más: obsérvese que en cada uno de los intervalos
. Pero hay algo más: obsérvese que en cada uno de los intervalos ![]() ,
, ![]() ,
, ![]() y
y ![]() , la región plana encerrada entre la curva y el eje
, la región plana encerrada entre la curva y el eje ![]() tiene idéntica área, con la única salvedad de que en dos de los intervalos, la región queda por debajo del eje
tiene idéntica área, con la única salvedad de que en dos de los intervalos, la región queda por debajo del eje ![]() (es decir, la función es negativa), mientras que en los otros dos, la región queda por encima (la función es positiva). Como la integral definida de una función mide el área con signo de la región plana encerrada entre la gráfica de la función y el eje
(es decir, la función es negativa), mientras que en los otros dos, la región queda por encima (la función es positiva). Como la integral definida de una función mide el área con signo de la región plana encerrada entre la gráfica de la función y el eje ![]() , basta una simple observación de su gráfica para deducir que
, basta una simple observación de su gráfica para deducir que
| y |
es decir, en ambos casos, las "áreas negativas" se compensan con las "áreas positivas". Pero aún podemos deducir más cosas; por ejemplo,
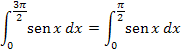 |
y | 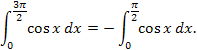 |
En general, basta tener presente cuál es el signo de las funciones seno y coseno en cada subintervalo de la forma ![]() , con
, con ![]() para poder expresar cualquier integral en
para poder expresar cualquier integral en ![]() como un múltiplo de la integral en
como un múltiplo de la integral en ![]() . Tal y como podemos ver en las gráficas de la Figura 1.5.1, el signo de ambas funciones es el que vemos representando en la Figura 1.5.2.
. Tal y como podemos ver en las gráficas de la Figura 1.5.1, el signo de ambas funciones es el que vemos representando en la Figura 1.5.2.
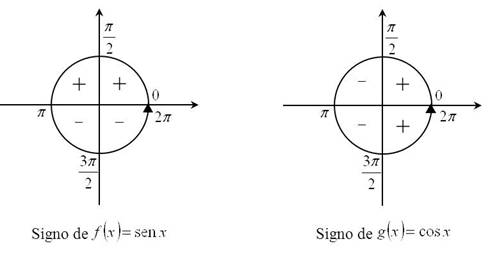
Figura 1.5.2 Signo de las funciones seno y coseno en el intervalo ![]() .
.
Las conclusiones que acabamos de extraer para las funciones seno y coseno por separado son extensibles a cualquier función de la forma ![]() , donde
, donde ![]() y
y ![]() son números enteros no negativos cualesquiera. La región del plano encerrada entre la gráfica de la función
son números enteros no negativos cualesquiera. La región del plano encerrada entre la gráfica de la función ![]() en el intervalo
en el intervalo ![]() y el eje
y el eje ![]() resulta siempre de la unión de cuatro trozos de igual área, correspondientes a los subintervalos
resulta siempre de la unión de cuatro trozos de igual área, correspondientes a los subintervalos ![]() ,
, ![]() ,
, ![]() y
y ![]() . Por tanto, basta conocer el área de uno de los trozos y analizar el signo de la función
. Por tanto, basta conocer el área de uno de los trozos y analizar el signo de la función ![]() en cada uno de los subintervalos anteriores para deducir el valor de la integral en
en cada uno de los subintervalos anteriores para deducir el valor de la integral en ![]() . Veamos dos ejemplos. En la Figura 1.5.3 podemos ver la gráfica de la curva
. Veamos dos ejemplos. En la Figura 1.5.3 podemos ver la gráfica de la curva ![]() en el intervalo
en el intervalo ![]() . En ella podemos apreciar que la región del plano comprendida entre dicha curva y el eje
. En ella podemos apreciar que la región del plano comprendida entre dicha curva y el eje ![]() se puede dividir en cuatro partes de igual área, correspondientes cada una de ellas a los subintervalos
se puede dividir en cuatro partes de igual área, correspondientes cada una de ellas a los subintervalos ![]() ,
, ![]() ,
, ![]() y
y ![]() .
.
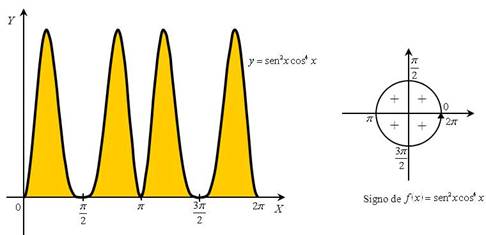
Figura 1.5.3 Gráfica y signo de la función ![]() en el intervalo
en el intervalo ![]() .
.
Además, cada uno de los trozos se encuentra por encima del eje ![]() , debido a que la función
, debido a que la función ![]() es siempre no negativa en
es siempre no negativa en ![]() . Por consiguiente, deducimos que
. Por consiguiente, deducimos que
![]()
El segundo ejemplo lo vemos en la Figura 1.5.4. Ahora tenemos la gráfica de la curva ![]() en el intervalo
en el intervalo ![]() . Podemos comprobar una vez más la existencia de cuatro trozos de igual área en la región del plano encerrada entre la curva y el eje
. Podemos comprobar una vez más la existencia de cuatro trozos de igual área en la región del plano encerrada entre la curva y el eje ![]() . Esto nos permite reducir la integral en el intervalo
. Esto nos permite reducir la integral en el intervalo ![]() a la integral en el intervalo
a la integral en el intervalo ![]() , sin más que analizar el signo de la función
, sin más que analizar el signo de la función ![]() en cada uno de los subintervalos
en cada uno de los subintervalos ![]() ,
, ![]() ,
, ![]() y
y ![]() . En
. En ![]() las funciones
las funciones ![]() y
y ![]() son positivas y, por tanto, la función
son positivas y, por tanto, la función ![]() es positiva. En
es positiva. En ![]() la función
la función ![]() es positiva, mientras que
es positiva, mientras que ![]() es negativa; por tanto, la función
es negativa; por tanto, la función ![]() es negativa. En
es negativa. En ![]() las funciones
las funciones ![]() y
y ![]() son negativas y, por tanto, la función
son negativas y, por tanto, la función ![]() es positiva. Por último, en
es positiva. Por último, en ![]() la función
la función ![]() es negativa, mientras que
es negativa, mientras que ![]() es positiva; por tanto, la función
es positiva; por tanto, la función ![]() es negativa. Como tenemos dos subintervalos en los que la función es positiva y dos en los que la función es negativa, deducimos que
es negativa. Como tenemos dos subintervalos en los que la función es positiva y dos en los que la función es negativa, deducimos que
![]()
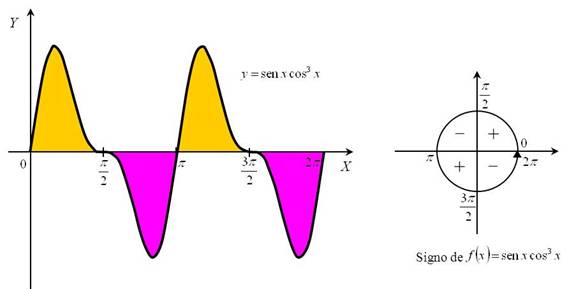
Figura 1.5.4 Gráfica y signo de la función ![]() en el intervalo
en el intervalo ![]() .
.
Llegados a este punto, cabría preguntarse cuál es el interés de reducir en este tipo de integrales el intervalo de integración a ![]() . La respuesta a este pregunta la podemos encontrar si observamos la Propiedad (3) de la función Beta de parámetros
. La respuesta a este pregunta la podemos encontrar si observamos la Propiedad (3) de la función Beta de parámetros ![]() y
y ![]() , que nos dice que
, que nos dice que
![]()
Volvamos sobre la integral de la función ![]() en el intervalo
en el intervalo ![]() . Según hemos visto, tenemos que
. Según hemos visto, tenemos que
![]()
La integral resultante tiene las mismas características que la función Beta. Se trata de identificar los exponentes del seno y del coseno, es decir, de encontrar los valores de ![]() y
y ![]() para los cuales se cumple que
para los cuales se cumple que
![]()
los cuales son ![]() y
y ![]() . En tal caso, tenemos que
. En tal caso, tenemos que
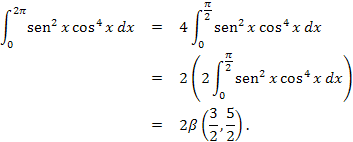
Finalmente, podemos calcular el valor de la función Beta haciendo uso de su relación con la función Gamma:
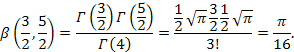
Por consiguiente, tenemos que
![]()
Ejemplo 1.5.1 Hallar las siguientes integrales definidas:
Resolución.
(a) El integrando es de la forma ![]() , con
, con ![]() y
y ![]() . En primer lugar debemos analizar el signo de la función en el intervalo
. En primer lugar debemos analizar el signo de la función en el intervalo ![]() . El análisis es inmediato en este caso, puesto que con independencia del signo de
. El análisis es inmediato en este caso, puesto que con independencia del signo de ![]() , cuando está elevado a potencia par se convierte en una función no negativa. Así pues,
, cuando está elevado a potencia par se convierte en una función no negativa. Así pues,
![]()
Una vez reducido el intervalo de integración a ![]() , buscamos identificar la integral con una función Beta. Para ello es necesario conocer los valores de los parámetros
, buscamos identificar la integral con una función Beta. Para ello es necesario conocer los valores de los parámetros ![]() y
y ![]() , cosa que hacemos resolviendo el sistema
, cosa que hacemos resolviendo el sistema
![]()
cuya solución es ![]() y
y ![]() . Así pues,
. Así pues,
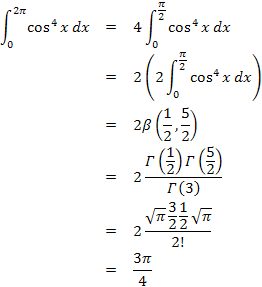
(b) La novedad de este ejemplo con respecto a los anteriores es que ahora el intervalo de integración es ![]() . En cualquier caso, debemos reducir el mismo al intervalo
. En cualquier caso, debemos reducir el mismo al intervalo ![]() , estudiando el signo de la función
, estudiando el signo de la función ![]() en
en ![]() . En
. En ![]() y en
y en ![]() la función
la función ![]() es positiva. Como además,
es positiva. Como además, ![]() es también positiva por tratarse de una potencia con exponente par, deducimos que la función
es también positiva por tratarse de una potencia con exponente par, deducimos que la función ![]() es positiva en ambos subintervalos. Por tanto,
es positiva en ambos subintervalos. Por tanto,
![]()
El segundo paso consiste en buscar la Beta correspondiente y, para ello, resolvemos el sistema
![]()
cuya solución es ![]() y
y ![]() . Por consiguiente,
. Por consiguiente,